Produkt (teoria kategorii)

Produkt – w teorii kategorii pojęcie będące uogólnieniem konstrukcji produktu kartezjańskiego zbiorów, produktu grup, czy produktu przestrzeni topologicznych; jest to „najogólniejszy” obiekt, mający kanoniczne rzuty do każdego z obiektów objętych tą konstrukcją (czynników). Konstrukcją dualną do produktu jest koprodukt.

Definicja

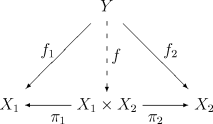
Obiekt ${\displaystyle X}$ nazywa się produktem obiektów ${\displaystyle X_{1}}$ oraz ${\displaystyle X_{2},}$ oznaczając go wtedy symbolem ${\displaystyle X_{1}\times X_{2},}$ wtedy i tylko wtedy, gdy spełnia następującą własność uniwersalną:

istnieją takie morfizmy ${\displaystyle \pi _{1}\colon X\to X_{1},\pi _{2}\colon X\to X_{2}}$ nazywane rzutami kanonicznymi, że dla dowolnego obiektu ${\displaystyle Y}$ i pary morfizmów ${\displaystyle f_{1}\colon Y\to X_{1},f_{2}\colon Y\to X_{2}}$ istnieje jednoznacznie wyznaczony morfizm ${\displaystyle f\colon Y\to X,}$ dla którego następujący diagram jest przemienny:

Jednoznacznie wyznaczony morfizm ${\displaystyle f}$ nazywa się produktem morfizmów ${\displaystyle f_{1}}$ oraz ${\displaystyle f_{2}}$ i oznacza się go symbolem ${\displaystyle \langle f_{1},f_{2}\rangle .}$ Powyższą definicję produktu dwóch obiektów można rozszerzyć biorąc dowolną rodzinę obiektów indeksowanych pewnym zbiorem ${\displaystyle I.}$ Obiekt ${\displaystyle X}$ nazywa się produktem rodziny ${\displaystyle \{X\}_{i}}$ obiektów wtedy i tylko wtedy, gdy

istnieją takie morfizmy ${\displaystyle \pi _{i}\colon X\to X_{i},}$ że dla dowolnego obiektu ${\displaystyle Y}$ oraz rodziny morfizmów ${\displaystyle f_{i}\colon Y\to X_{i}}$ indeksowanej zbiorem ${\displaystyle I}$ istnieje jednoznacznie wyznaczony morfizm ${\displaystyle f\colon Y\to X,}$ dla którego następujący diagram jest przemienny dla wszystkich ${\displaystyle i\in I{:}}$

Produkt oznacza się wtedy symbolem ${\displaystyle \prod _{i\in I}X_{i};}$ jeżeli ${\displaystyle I=\{1,\dots ,n\},}$ to na oznaczenie produktu obiektów zwykle używa się oznaczenia ${\displaystyle X_{1}\times \cdots \times X_{n},}$ a produkt morfizmów często oznacza się wtedy ${\displaystyle \langle f_{1},\dots ,f_{n}\rangle .}$

Produkt można również zdefiniować wyłącznie za pomocą równań – oto przykład dla produktu dwóch obiektów:

• istnienie ${\displaystyle f}$ zachodzi dzięki operacji ${\displaystyle \langle \cdot ,\cdot \rangle ;}$
• przemienność powyższych diagramów wynika z równości ${\displaystyle \pi _{i}\circ \langle f_{1},f_{2}\rangle =f_{i}}$ dla wszystkich ${\displaystyle f_{1},f_{2}}$ oraz ${\displaystyle i=1,2;}$
• jednoznaczność ${\displaystyle f}$ wynika z równości ${\displaystyle \langle \pi _{1}\circ f,\pi _{2}\circ f\rangle =f}$ dla wszystkich ${\displaystyle f.}$

Produkt można także opisać za pomocą granicy: rodzinę obiektów można postrzegać jako diagram bez morfizmów; okazuje się, że traktując go jako funktor, mianowicie funktor ze zbioru ${\displaystyle I}$ rozpatrywanego jako kategoria dyskretna, to definicja produktu pokrywa się z definicją granicą, przy czym ${\displaystyle \{f\}_{i}}$ pełni rolę stożka, a rzuty są granicą (stożkiem granicznym).

Zamiast granicy można użyć własności uniwersalnej; dla porównania: w tym przypadku ${\displaystyle J}$ jest kategorią dyskretną z dwoma obiektami, a ${\displaystyle C^{J}}$ to po prostu kategoria produktowa ${\displaystyle C\times C,}$ przy czym funktor diagonalny ${\displaystyle \Delta \colon C\to C\times C}$ przypisuje każdemu z obiektów ${\displaystyle X}$ parę uporządkowaną ${\displaystyle (X,X),}$ a każdemu morfizmowi ${\displaystyle f}$ parę ${\displaystyle (f,f)}$ – produkt ${\displaystyle X_{1}\times X_{2}}$ w ${\displaystyle C}$ dany jest za pomocą morfizmu uniwersalnego z funktora ${\displaystyle \Delta }$ w obiekt ${\displaystyle (X_{1},X_{2})}$ w ${\displaystyle C\times C}$ – wspomniany morfizm uniwersalny składa się z obiektu ${\displaystyle X}$ należącego do kategorii ${\displaystyle C}$ i morfizmu ${\displaystyle (X,X)\to (X_{1},X_{2})}$ zawierającego rzuty.

Przykłady

• W kategorii Set produktem zbiorów ${\displaystyle A}$ i ${\displaystyle B}$ jest iloczyn kartezjański ${\displaystyle A\times B}$ wraz z rzutami ${\displaystyle \pi _{1}((x,y))=x}$ i ${\displaystyle \pi _{2}((x,y))=y.}$
• W kategorii Grp produktem jest iloczyn kartezjański grup wraz z rzutami.
• W kategorii Top produkt jest iloczynem kartezjańskim przestrzeni z topologią produktową.
• W posecie ${\displaystyle (P,\leqslant ),}$ traktowanym jako kategoria, produktem elementów ${\displaystyle a,b}$ jest ${\displaystyle \inf\{a,b\}.}$

Zobacz też

• funktory sprzężone
• koprodukt
• zagadnienia jednoznacznej faktoryzacji