Trygonometria

Wszystkie funkcje trygonometryczne kąta θ mogą zostać geometrycznie skonstruowane w odniesieniu do okręgu ze środkiem w punkcie O

Trygonometria (łac. trigonometria, od trigonum: z gr. τρίγωνον trigōnon, neutr. od τρίγωνος trigōnos, „trójrożny, trójkątny”, od -γωνον -gōnon, od γωνία gōnia, „róg, kąt”; spokr. z γόνυ gónu, „kolano” oraz: łac. -metria, od gr. μετρεῖν metrein, „mierzyć”, od μέτρον metron, „miara, kij/pręt mierniczy”) – dział matematyki, którego przedmiotem badań są związki miarowe między bokami i kątami trójkątów oraz funkcje trygonometryczne^[1]. Trygonometria powstała i rozwinęła się głównie w związku z zagadnieniami pomiarów na powierzchni Ziemi oraz potrzebami żeglugi morskiej (określenia położenia i kierunku przy pomocy ciał niebieskich). Na rozwój trygonometrii miały też wpływ badania astronomiczne.

Historia

Egipt i Babilon

Tabliczka Plimpton 322

W starożytnym Egipcie i Babilonie od wieków znano twierdzenia dotyczące stosunków boków trójkątów podobnych. Jednak społeczeństwa przed Grekami prawdopodobnie nie wynalazły idei miary kąta i w konsekwencji badały tylko boki trójkąta^[2].

Niektórzy badacze uważają, że starożytni Babilończycy zapisali pismem klinowym na tabliczce Plimpton 322, powstałej ok. 1800–1900 lat p.n.e., tablicę sekansów^[3]. Jednakże według innych interpretacji mogły to być tablice trójek pitagorejskich^[4][5] albo rozwiązanie równania kwadratowego^[6][7].

Starożytna Grecja

Cięciwa łuku utworzonego przez dany kąt

Średniowieczne przedstawienie Klaudiusza Ptolemeusza

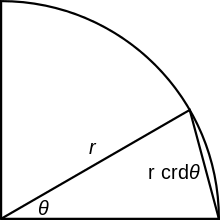
Matematycy starożytnej Grecji znali pojęcie cięciwy. Dla danego okręgu i jego części (łuku) cięciwa jest prostą, która przecina okrąg na końcach łuku. Symetralna odcinka cięciwy mieszczącego się wewnątrz koła przechodzi przez jego środek i dzieli łuk (i tym samym kąt) na pół. Połowa długości cięciwy to dla okręgu jednostkowego sinus połowy kąta, czyli ${\displaystyle {\mbox{crd}}\ \theta =2\sin {\tfrac {\theta }{2}}.}$ Wiele z twierdzeń trygonometrycznych było znanych starożytnym Grekom, jednak w postaci odpowiedników operujących długościami łuków i cięciw, a nie miarami kątów i stosunkami długości boków trójkąta^[8].

Jakkolwiek w dziełach Euklidesa i Archimedesa nie było trygonometrii w ścisłym tego słowa znaczeniu, są jednak twierdzenia zaprezentowane w geometrycznej formie, które stanowią odpowiedniki pewnych trygonometrycznych praw i wzorów^[2]. Na przykład propozycje XII i XIII z Księgi II Elementów są tożsame ze wzorem cosinusów odpowiednio dla kątów rozwartych i ostrych. Twierdzenia dotyczące długości cięciw są natomiast zastosowaniem wzoru sinusów. Jedno z twierdzeń Archimedesa jest zaś odpowiednikiem wzoru na sinus sumy i różnicy kątów^[2]. Matematycy za czasów Arystarcha z Samos dla celów obliczeniowych używali m.in. twierdzenia mówiącego, iż (we współczesnej notacji) ${\displaystyle {\tfrac {\sin \alpha }{\sin \beta }}<{\tfrac {\alpha }{\beta }}<{\tfrac {\operatorname {tg} \alpha }{\operatorname {tg} \beta }}}$ dla ${\displaystyle 0^{\circ }<\beta <\alpha <90^{\circ }}$^[9].

Pierwsze tablice trygonometryczne zostały prawdopodobnie skompilowane przez Hipparcha (180–125 p.n.e.)^[10]. Hipparch jako pierwszy ułożył tablice odpowiadających sobie długości cięciwy i łuku dla różnych kątów^[10][11].

Jakkolwiek nie wiadomo dokładnie, kiedy zaczęto używać podziału kąta pełnego na 360 stopni, przypuszczalnie nastąpiło to wkrótce po napisaniu przez Arystarcha z Samos dzieła O rozmiarach i odległościach Słońca i Księżyca ok. 260 p.n.e., gdyż mierzył on kąty w ułamkach kąta prostego^[9]. Prawdopodobnie podział kąta pełnego na 360 stopni spopularyzował się głównie dzięki Hipparchowi i jego tablicy cięciw. Hipparch mógł podchwycić ideę takiego podziału u Hipsikla, który wcześniej dzielił dobę na 360 części, zapewne wzorując się na babilońskich astronomach^[10]. W starożytnej astronomii ekliptyka została podzielona na 12 „znaków zodiaku” lub 36 dekanów. Roczny cykl około 360 dni można było otrzymać, dzieląc każdy znak na 30 części i każdy dekan na 10 części^[12]. To dzięki używanemu w Babilonii sześćdziesiątkowemu systemowi liczbowemu każdy stopień został podzielony na 60 minut kątowych, a każda minuta na 60 sekund kątowych^[12].

Menelaos z Aleksandrii (ok. 100 n.e.) napisał trzy księgi pod tytułem Sphaerica. W Księdze I sformułował dla trójkątów sferycznych odpowiedniki twierdzeń dotyczących trójkątów na płaszczyźnie^[8]. Sformułował również twierdzenie nieposiadające odpowiednika na płaszczyźnie euklidesowej, mówiące, że dwa trójkąty sferyczne są przystające, jeśli odpowiednie ich kąty mają równe miary (utożsamiał przy tym symetryczne wersje trójkątów sferycznych)^[8]. Menelaos zauważył także, że suma kątów wewnętrznych trójkąta sferycznego jest zawsze większa od 180°^[8]. Księga II Sphaerica dotyczyła zastosowań geometrii sferycznej do astronomii. Księga III zawierała „twierdzenie Menelausa”^[8].

Później Klaudiusz Ptolemeusz (ok. 90 – ok. 168 n.e.) rozbudował w swoim dziele Almagest koncepcję „cięciw na okręgu” Hipparcha. Trzynasta księga Almagestu była znaczącą starożytną pracą w dziedzinie trygonometrii^[13]. Jedno z jej twierdzeń jest dziś znane jako twierdzenie Ptolemeusza. Szczególny przypadek twierdzenia Ptolemeusza pojawia się także w Propozycji XCIII dzieła Euklidesa. Twierdzenie Ptolemeusza prowadzi do równoważnika wzorów na sinus i cosinus sumy i różnicy, choć oczywiście wyrażonych w języku cięciw, a nie funkcji. Ptolemeusz wyprowadził później ekwiwalent wzoru

${\displaystyle \sin ^{2}{\tfrac {x}{2}}={\tfrac {1-\cos x}{2}}.}$

Ptolemeusz używał tych wyników do stworzenia tablic trygonometrycznych, choć nie wiadomo, czy nie były one wyprowadzone z dzieła Hipparcha^[13].

Ani tablice Hipparcha, ani Ptolemeusza nie przetrwały do czasów współczesnych, choć dzięki wzmiankom u innych autorów nie ma wątpliwości, że istniały^[14].

Średniowieczne Indie

Posąg Aryabhaty

Kolejny istotny postęp w trygonometrii został dokonany w Indiach. Indyjski matematyk i astronom Aryabhata (476–550 n.e.) w swoim dziele Aryabhata-Siddhanta po raz pierwszy zdefiniował sinus w znanej dzisiaj formie związku między połową kąta i połową cięciwy, a także cosinus, sinus versus i arcus sinus. Jego dzieła zawierają najwcześniejsze tablice trygonometryczne, które przetrwały do dzisiaj, z wartościami funkcji sinus i sinus versus co 3.75° stopnia od 0° do 90°, z dokładnością do czterech miejsc znaczących. Jego nazwy na sinus i cosinus stały się podstawą nazw używanych dzisiaj (zobacz Definicja na okręgu jednostkowym i etymologia nazw funkcji trygonometrycznych).

Inni hinduscy matematycy rozwinęli później pracę Aryabhaty. W VI wieku n.e. Varahamihira używał wzorów:

${\displaystyle \sin ^{2}x+\cos ^{2}x=1,}$

${\displaystyle \sin x=\cos \left({\tfrac {\pi }{2}}-x\right),}$

${\displaystyle {\tfrac {1-\cos(2x)}{2}}=\sin ^{2}x.}$

W VII wieku Bhaskara I stworzył wzór pozwalający na przybliżone obliczanie sinusa dla kąta ostrego bez tablic (z błędem mniejszym od 1,9%):

${\displaystyle \sin x\approx {\tfrac {16x(\pi -x)}{5\pi ^{2}-4x(\pi -x)}},\qquad 0\leqslant x\leqslant {\tfrac {\pi }{2}}.}$

W końcu VII wieku, Brahmagupta wyprowadził wzór:

${\displaystyle 1-\sin ^{2}x=\cos ^{2}x=\sin ^{2}\left({\tfrac {\pi }{2}}-x\right)}$

oraz tzw. wzór interpolacyjny Brahmagupty:

${\displaystyle f(a+xh)\approx f(a)+x\left({\tfrac {\Delta f(a)+\Delta f(a-h)}{2}}\right)+{\tfrac {x^{2}\Delta ^{2}f(a-h)}{2}},}$

który pozwolił mu na stablicowanie wartości sinusa^[15].

Świat islamu

Al-Chuwarizmi sportretowany na radzieckim znaczku pocztowym

Prace matematyków hinduskich zostały później przetłumaczone i rozszerzone w świecie muzułmańskim przez arabskich i perskich matematyków. W IX wieku Muhammad ibn Musa al-Chuwarizmi obliczył dokładne tablice sinusa i cosinusa i pierwsze w historii tablice tangensa.

W X wieku islamscy matematycy używali wszystkich sześciu funkcji trygonometrycznych z secansem i cosecansem włącznie, co wiadomo dzięki pracy autorstwa Abu al-Wafa. Abu al-Wafa stworzył tablice sinusa z krokiem 0,25° i dokładnością 8 cyfr dziesiętnych, a także dokładne tablice tangensa. Zauważył również tożsamość:

${\displaystyle \sin 2x=2\sin x\cos x.}$

Wszystkie te wczesne wyniki trygonometryczne powstawały głównie w związku z pracami astronomicznymi, pierwsze traktaty wyłącznie o trygonometrii opublikowali zapewne Bhāskara Acārya i Nasir ad-Din Tusi w XIII wieku. Nasir ad-Din Tusi sformułował i udowodnił twierdzenie sinusów, sklasyfikował też sześć różnych przypadków prostokątnych trójkątów sferycznych.

W XIV wieku Ghijas ad-Din Kaszi stworzył tablice sinusa z dokładnością do czterech cyfr sześćdziesiątkowych (odpowiednik 8 miejsc dziesiętnych) dla każdego stopnia z dodatkowymi poprawkami do obliczania wartości dla każdej minuty kątowej. Uług Beg (XV wiek) także podał dokładne tablice sinusa i tangensa sięgające 8 miejsc dziesiętnych.

Średniowieczne Chiny

Guo Shoujing (1231–1316)

Tablice sinusów Aryabhaty zostały przetłumaczone na chiński i umieszczone w klasycznym dziele Kaiyuan Zhan Jing, skompilowanym w 718 roku w okresie dynastii Tang^[16]. Jakkolwiek Chińczycy celowali w innych dziedzinach matematyki, takich jak stereometria, czy algebra, to wczesne formy trygonometrii nie rozpowszechniły się tak szybko jak w przypadku Greków, Hindusów i muzułmanów^[17]. Powoli ten stan zaczął się zmieniać w okresie dynastii Song (960–1279), kiedy chińscy matematycy zaczęli kłaść większy nacisk na potrzeby geometrii sferycznej^[16]. Na przykład Shen Kuo (1031–1095) używał funkcji trygonometrycznych do rozwiązywania problemów matematycznych z cięciwami i łukami^[16]. Jak twierdzą historycy L. Gauchet i Joseph Needham, inny matematyk, Guo Shoujing (1231–1316) używał trygonometrii sferycznej w kalkulacjach kalendarzowych i astronomicznych^[18][16].

Renesansowa Europa

Regiomontanus był prawdopodobnie pierwszym europejskim matematykiem, który traktował trygonometrię jako oddzielną dyscyplinę matematyczną. Napisał w 1464 De triangulis omnimodus, a później Tabulae directionum.

Funkcję secans w Europie wprowadził Mikołaj Kopernik w dziele De revolutionibus orbium coelestium (1543)^[19], choć arabscy matematycy używali jej prawdopodobnie już w IX wieku^[20].

Francesco Maurolico w 1555 używał zapisu sinus^[21], w 1583 J. Finck użył określeń tangens^[22] oraz sekans^[20]. Edmund Gunter w 1620 roku użył słowa cotangens^[23], w 1624 roku wprowadził oznaczenie sin x^[21] oraz tan x^[22], a w 1636 cosi x oraz słowo cosinus (zamiast complementi sinus)^[24]. François Viète w 1590 znalazł wzór na ${\displaystyle \cos nx}$^[24].

W 1595 Bartłomiej Pitiscus użył po raz pierwszy terminu „trygonometria” w swoim dziele Trigonometria: sive de solutione triangulorum Tractatus brevis et perspicuus (1595, Heidelberg).

Opus palatinum de triangulis autorstwa Retyka, było prawdopodobnie pierwszą definicją funkcji trygonometrycznych w terminach trójkątów prostokątnych zamiast okręgów jednostkowych; ta praca została dokończona przez Valentina Otho, studenta Rheticusa w roku 1596.

Isaac Newton w 1665 znalazł rozwinięcie funkcji sinus^[21] i cosinus^[24] w szereg, a Leonhard Euler w 1734 rozwinięcie funkcji sinus w iloczyn nieskończony^[21].

W XVII wieku Isaac Newton i James Stirling stworzyli wzór interpolacyjny Newtona-Stirlinga dla funkcji trygonometrycznych.

W 1770 Johann Heinrich Lambert znalazł reprezentację tangensa w postaci ułamka łańcuchowego^[22].

Historia analizy trygonometrycznej

Madhava (około roku 1400) stworzył podwaliny analizy matematycznej funkcji trygonometrycznych, odkrywając rozwinięcie funkcji w szeregi nieskończone. Badał on koncepcje szeregów potęgowych oraz pewnego szeregu, nazwanego później w Europie szeregiem Taylora i obliczył rozwinięcia sinusa, cosinusa, tangensa i cotangensa. Używając aproksymacji sinusa i cosinusa szeregiem Taylora, stworzył tablice sinusa z 12 miejscami znaczącymi i cosinusa z 9 miejscami znaczącymi. Podał także rozwinięcie π w szereg potęgowy. Jego prace były rozwijane przez jego następców ze szkoły astronomicznej w Kerala aż do XVI wieku^[25][26].

Introductio in analysin infinitorum Leonharda Eulera z 1748 roku stworzyło grunt dla analitycznego traktowania funkcji trygonometrycznych w Europie, definiując je jako nieskończone szeregi i wprowadzając „wzór Eulera”. Euler używał skrótów zbliżonych do dzisiejszych: sin., cos., tang., cot., sec., i cosec.

James Gregory, a następnie Brook Taylor badali szeregi, znane dziś jako szeregi Taylora. Ten ostatni znalazł rozwinięcia i aproksymacje wszystkich sześciu funkcji trygonometrycznych. Duże znaczenie na tym polu miały również prace Colina Maclaurina.

Zobacz też

• funkcje odwrotne do trygonometrycznych
• tożsamości trygonometryczne – lista najważniejszych wzorów
• trygonometryczne wzory redukcyjne
• twierdzenie sinusów, twierdzenie cosinusów, twierdzenie tangensów – twierdzenia przydatne przy rozwiązywaniu zadań dotyczących trójkątów

Przypisy

Bibliografia

• Carl B. Boyer: A History of Mathematics. Wyd. Second Edition. John Wiley & Sons, Inc., 1991. ISBN 0-471-54397-7.
• J.J. O’Connor, E.F. Robertson: Madhava of Sangamagramma (ang.). W: MacTutor History of Mathematics Archive [on-line]. 2000.
• J.J. O’Connor, E.F. Robertson: Trigonometric functions (ang.). W: MacTutor History of Mathematics Archive [on-line]. 1996.
• L. Gauchet: Note Sur La Trigonométrie Sphérique de Kouo Cheou-King. 1917.
• George G. Joseph: The Crest of the Peacock: Non-European Roots of Mathematics. Wyd. 2. Londyn: Penguin Books, 2000. ISBN 0-691-00659-8.
• Joseph Needham: Science and Civilization in China: tom 3, Mathematics and the Sciences of the Heavens and the Earth. Taipei: Caves Books, Ltd., 1986.
• Ian G. Pearce: Madhava of Sangamagramma (ang.). W: MacTutor History of Mathematics Archive [on-line]. 2002. [dostęp 2009-03-24]. [zarchiwizowane z tego adresu (2006-05-05)].
• R.P. Kostecki: Krótka historia matematyki